MATEMÁTICA II
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Se f(x) = 3x - 4 e f(g(x)) = x + 4, então o valor de g(1) é exatamente:
3
2
4
1
0
A aplicação de reajuste salarial está intimamente ligado ao estudo da função composta.
Considere a situação a seguir:
Uma empresa de cosméticos oferece aos seus funcionários um salário mensal de R$ 1180,00 para atendente de caixa. O proprietário ainda garante que todos funcionários vão ter direito a dois reajustes anuais de:
5% ao final do 1º semestre;
5% ao final do 2º semestre;
É correto afirmar:
(I) Depois dos reajustes o salário será de R$ 1.298,00;
(II) A função composta dos salários é dada por g(f(x)) = 1,1025x;
(III) Ao final do 2º semestre o salário será de R$ 1.300,95;
(IV) A função composta dos salários é dada por gof = 2,1x;
(I) e (IV) estão corretas.
(II) e (IV) estão corretas.
Todas estão corretas.
(II) e (III) estão corretas.
(I) e (II) estão corretas.
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-1 ) + f(0) + f|(1) então N é igual a:
14
13
17
9
16
Considere o esboço gráfico da função f(x) a abaixo:
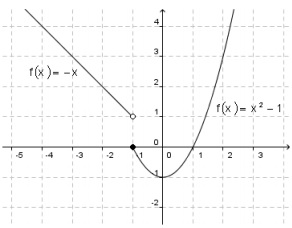
O valor de f(2) - f(-2) + f(-1)+ f(0) - f(1) é igual a:
3
5
-1
0
-3
Equação é uma expressão algébrica com uma ou mais incógnitas que possui uma igualdade, então, podemos dizer que uma equação modular possui essas mesmas características, sendo que a incógnita dessa equação terá que estar dentro de um módulo.
Para resolver uma equação modular deve-se seguir a definição de módulo de um número real:  , se
, se 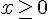 ou
ou  , se
, se  .
.
Resolva  e marque a opção que representa o conjunto solução.
e marque a opção que representa o conjunto solução.





Inequação modular é toda inequação cuja incógnita aparece em módulo.
Podemos utilizar as propriedades a seguir para resolver:
|x| > a → x < a ou x > a.|x| < a → a < x < a.|x| ≤ a → a ≤ x ≤ a.|x| ≥ a → x ≤ a ou x ≥ a.|x a| ≤ b → b ≤ x a ≤ b → a b ≤ x ≤ a + bResolva e assinale a opção que indica o conjunto solução da inequação |x2 + 4x - 6| > 15.
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547
3
2
4
1
0
A aplicação de reajuste salarial está intimamente ligado ao estudo da função composta.
Considere a situação a seguir:
Uma empresa de cosméticos oferece aos seus funcionários um salário mensal de R$ 1180,00 para atendente de caixa. O proprietário ainda garante que todos funcionários vão ter direito a dois reajustes anuais de:
5% ao final do 1º semestre;
5% ao final do 2º semestre;
É correto afirmar:
(I) Depois dos reajustes o salário será de R$ 1.298,00;
(II) A função composta dos salários é dada por g(f(x)) = 1,1025x;
(III) Ao final do 2º semestre o salário será de R$ 1.300,95;
(IV) A função composta dos salários é dada por gof = 2,1x;
(I) e (IV) estão corretas.
(II) e (IV) estão corretas.
Todas estão corretas.
(II) e (III) estão corretas.
(I) e (II) estão corretas.
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-1 ) + f(0) + f|(1) então N é igual a:
14
13
17
9
16
Considere o esboço gráfico da função f(x) a abaixo:

O valor de f(2) - f(-2) + f(-1)+ f(0) - f(1) é igual a:
3
5
-1
0
-3
Equação é uma expressão algébrica com uma ou mais incógnitas que possui uma igualdade, então, podemos dizer que uma equação modular possui essas mesmas características, sendo que a incógnita dessa equação terá que estar dentro de um módulo.
Para resolver uma equação modular deve-se seguir a definição de módulo de um número real:  , se
, se 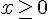 ou
ou  , se
, se  .
.
Resolva  e marque a opção que representa o conjunto solução.
e marque a opção que representa o conjunto solução.





Inequação modular é toda inequação cuja incógnita aparece em módulo.
Podemos utilizar as propriedades a seguir para resolver:
|x| > a → x < a ou x > a.|x| < a → a < x < a.|x| ≤ a → a ≤ x ≤ a.|x| ≥ a → x ≤ a ou x ≥ a.|x a| ≤ b → b ≤ x a ≤ b → a b ≤ x ≤ a + bResolva e assinale a opção que indica o conjunto solução da inequação |x2 + 4x - 6| > 15.
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547
(I) e (IV) estão corretas.
(II) e (IV) estão corretas.
Todas estão corretas.
(II) e (III) estão corretas.
(I) e (II) estão corretas.
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-1 ) + f(0) + f|(1) então N é igual a:
14
13
17
9
16
Considere o esboço gráfico da função f(x) a abaixo:

O valor de f(2) - f(-2) + f(-1)+ f(0) - f(1) é igual a:
3
5
-1
0
-3
Equação é uma expressão algébrica com uma ou mais incógnitas que possui uma igualdade, então, podemos dizer que uma equação modular possui essas mesmas características, sendo que a incógnita dessa equação terá que estar dentro de um módulo.
Para resolver uma equação modular deve-se seguir a definição de módulo de um número real:  , se
, se 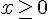 ou
ou  , se
, se  .
.
Resolva  e marque a opção que representa o conjunto solução.
e marque a opção que representa o conjunto solução.





Inequação modular é toda inequação cuja incógnita aparece em módulo.
Podemos utilizar as propriedades a seguir para resolver:
|x| > a → x < a ou x > a.|x| < a → a < x < a.|x| ≤ a → a ≤ x ≤ a.|x| ≥ a → x ≤ a ou x ≥ a.|x a| ≤ b → b ≤ x a ≤ b → a b ≤ x ≤ a + bResolva e assinale a opção que indica o conjunto solução da inequação |x2 + 4x - 6| > 15.
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547
14
13
17
9
16
Considere o esboço gráfico da função f(x) a abaixo:

O valor de f(2) - f(-2) + f(-1)+ f(0) - f(1) é igual a:
3
5
-1
0
-3
Equação é uma expressão algébrica com uma ou mais incógnitas que possui uma igualdade, então, podemos dizer que uma equação modular possui essas mesmas características, sendo que a incógnita dessa equação terá que estar dentro de um módulo.
Para resolver uma equação modular deve-se seguir a definição de módulo de um número real:  , se
, se 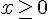 ou
ou  , se
, se  .
.
Resolva  e marque a opção que representa o conjunto solução.
e marque a opção que representa o conjunto solução.





Inequação modular é toda inequação cuja incógnita aparece em módulo.
Podemos utilizar as propriedades a seguir para resolver:
|x| > a → x < a ou x > a.|x| < a → a < x < a.|x| ≤ a → a ≤ x ≤ a.|x| ≥ a → x ≤ a ou x ≥ a.|x a| ≤ b → b ≤ x a ≤ b → a b ≤ x ≤ a + bResolva e assinale a opção que indica o conjunto solução da inequação |x2 + 4x - 6| > 15.
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547

3
5
-1
0
-3
Equação é uma expressão algébrica com uma ou mais incógnitas que possui uma igualdade, então, podemos dizer que uma equação modular possui essas mesmas características, sendo que a incógnita dessa equação terá que estar dentro de um módulo.
Para resolver uma equação modular deve-se seguir a definição de módulo de um número real:  , se
, se 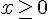 ou
ou  , se
, se  .
.
Resolva  e marque a opção que representa o conjunto solução.
e marque a opção que representa o conjunto solução.





Inequação modular é toda inequação cuja incógnita aparece em módulo.
Podemos utilizar as propriedades a seguir para resolver:
|x| > a → x < a ou x > a.|x| < a → a < x < a.|x| ≤ a → a ≤ x ≤ a.|x| ≥ a → x ≤ a ou x ≥ a.|x a| ≤ b → b ≤ x a ≤ b → a b ≤ x ≤ a + bResolva e assinale a opção que indica o conjunto solução da inequação |x2 + 4x - 6| > 15.
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547
Inequação modular é toda inequação cuja incógnita aparece em módulo.
Podemos utilizar as propriedades a seguir para resolver:
|x| > a → x < a ou x > a.|x| < a → a < x < a.|x| ≤ a → a ≤ x ≤ a.|x| ≥ a → x ≤ a ou x ≥ a.|x a| ≤ b → b ≤ x a ≤ b → a b ≤ x ≤ a + bResolva e assinale a opção que indica o conjunto solução da inequação |x2 + 4x - 6| > 15.
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547
S = [ -7, 3 ]
S = [ -5, 2 ]
S = ] -7, 3 ]
S = ] -7, 3 [
S = ] -5, 2 [
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere %7D%3D%7B%7B25%7D%7D%5E%7B%7B%7B2%7D-%7B0%7D%2C%7B125%7D%7BT%7D%7D%7D) a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
a quantidade Q(t) de substância em miligramas que permanece no paciente, t horas após a aplicação.
A quantidade de substância que permanece no paciente após 6 horas é aproximadamente:
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas
A população de uma cidade cresce aproximadamente 4,166...% ao ano, ou seja 1/24 ao ano. O tempo, em anos, necessário para que a população seja o dobro da população atual é de aproximadamente
Dados:
log2 = 0,3010299956
log3 = 0,4771212547
59,75 miligramas
49,55 miligramas
55,90 miligramas
65,90 miligramas
61,50 miligramas